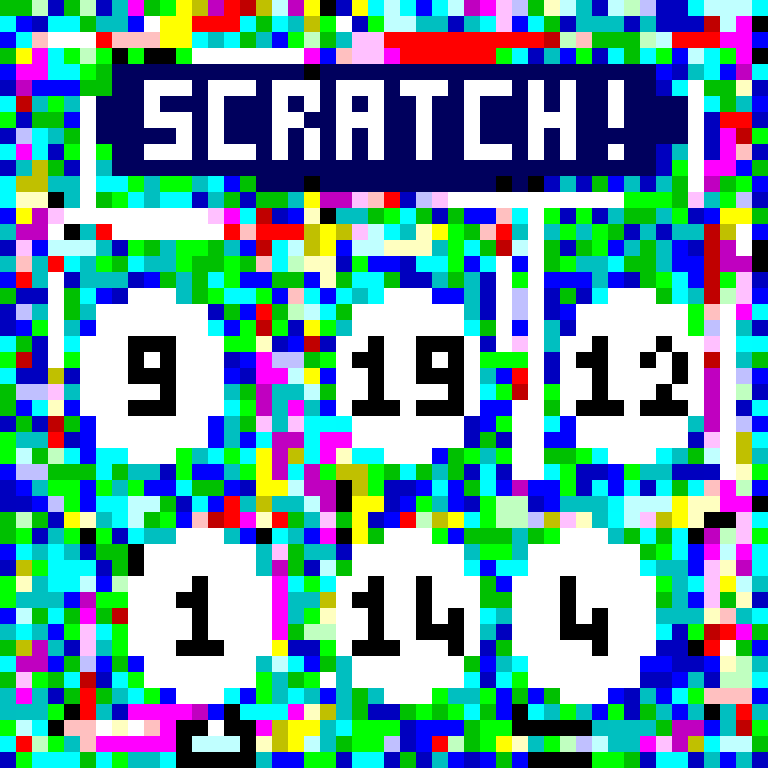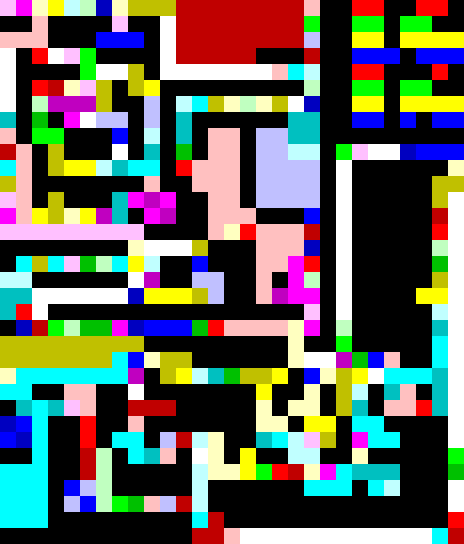On Day 4, we journey up the gondola lift to Island Island and meet an elf with a pile of colourful square scratchcards. They look just like this one, which also happens to be a valid Piet program that solves Part 2 of today’s problem:
It’s only 48x48 pixels, so here it is with 16x zoom:
In 2023, my solution for Day 2 was in Piet (David Morgan-Mar’s website, esolang), a stack-based language where the source code is an image, and instructions are encoded by transitions in colours as execution moves around the image. At the time, I wrote the instructions as text, and used a Piet assembler to construct an image. I don’t think I would have finished within 24h without that, but it left me wanting to construct a Piet program by hand, and so I was delighted when I realised this day’s problem was suitable.
Part 1
Our input is a sequence of cards, where each card has a set of winning numbers (which I will call “card numbers”) and a list of numbers you have (which I will call “test numbers”). We need to find out how many of our test numbers are in the set of card numbers to determine how many points each card is worth (one point for the first match, and then doubling for each subsequent match) and output the sum of all cards’ points.
Piet is a stack-based language, and it provides operators for:
- basic stack manipulation: push a positive number on top of the stack, pop off the top of the stack, duplicate the top of the stack
- arithmetic: add, subtract, multiply, divide and mod for taking the remainder, which all pop the top two numbers on the stack and push their result
- comparison: not (replaces the top of the stack with 1 if nonzero, else 0), and greater (replaces the top two values of the stack with 1 if the second is greater than the top, else 0)
- data-driven movement: pointer pops the top value of the stack and rotates the direction pointer by that amount, and switch does the same for the codel chooser
- data-driven stack manipulation: roll pops the top two values of the stack and uses them to rotate a section of the stack by a certain amount
- I/O: in and out do what you expect, but there are variants for characters (specified as Unicode, but with no encoding) or numbers (but exactly what is consumed from STDIN is undefined).
My approach to constructing a Piet program is structurally similar to what I did for Brainfuck in Day 1: write the algorithm, decompose that into a lower-level representation and then implement in the low-level language. For Piet, I’ll write the algorithm, decompose it into basic blocks and then lay out those basic blocks as an image.
Here’s the high-level algorithm (in pseudo-Python):
total = 0
for each line in STDIN:
STDIN.discard("Card {N}: ")
# read the winning numbers
card_numbers = []
while STDIN.read(1) == " " (or not "|"):
n = parse_integer(STDIN.read(2))
card_numbers.append(n)
# test how many numbers match
matches = 0
while STDIN.read(1) == " " (or not "\n"):
test_number = parse_integer(STDIN.read(2))
for each card_number in card_numbers:
if card_number == test_numbers:
matches += 1
break
# convert the number of matches to points
points = 0
if matches > 0:
points = 1
matches -= 1
while matches > 0:
points *= 2
matches -= 1
total += points
print(total)
The next step is to convert this into basic blocks, where each block contains a sequence of Piet instructions that is run in sequence and ends with an unconditional jump to another block, a conditional jump (zero or nonzero) to two1 other blocks, or by terminating the program.
This representation is too verbose for this blog post, so I’ll leave the link
for interested readers,
and just call out a few interesting2 aspects.
I wrote this representation in Python, where each basic
block is a function that calls functions implementing the Piet instructions and
ends in an unconditional jump (calling another basic block function), a
conditional jump (calling a jnz function with the functions to call if the top
value is zero or nonzero) or doing nothing (which results in termination).
Implementing the framework for this is less than 100 lines of code, but does
require a sys.setrecursionlimit call for non-trivial inputs, so not the kind
of code you want to put into production, but I think we’d already passed that
point by the second paragraph of this blog post.
Anyhow, we start by setting total to zero:
def bb0_init_total():
push(1)
not_()
bb1_check_eof()
We can’t just push(0) because the value pushed is the size (number of
pixelscodels) of the previous colour block, so instead we push a
positive number (any will do, but one takes the least space) onto the stack
and then use not to turn it into a zero. We then jump to bb1_check_eof,
which implements the looping behaviour of for each line in STDIN: by consuming
a character from STDIN and testing if we reached the end. This also consumes
the 'C' from "Card {N}: ", but that’s okay.
def bb1_check_eof():
# inchr: If no input is waiting on STDIN, this is an error and the command
# is ignored.
# To detect EOF, we push 0 onto the stack, then call inchr.
push(1)
not_()
inchr()
# If we read nothing, we will have a zero on the stack.
not_()
jnz(bb23_exit, bb2_not_eof)
In Piet, any instructions that cannot be performed (including attempting to read
from STDIN when no input is available) are ignored and do nothing.
So if inchr reads any character (except NUL),
we’ll have a non-zero value on top of the stack,
which not will turn into a zero, and jnz will jump to bb2_not_eof.
If it does nothing, not will turn the zero we put into the stack into a one,
and jnz will jump to bb23_exit.
That’s all well and good, but let’s skip ahead to the parsing code. We need to
implement STDIN.discard("Card {N}: "), where {N} can be any (space-prefixed)
integer. To achieve this without excessive instructions, we’re going to assume
our input is well-formed. This is not an assumption one should usually make,
but in this situation, we only have two inputs our program is expected to handle
(the example and the actual input), which are well-formed, so we can make this
assumption.
Having assumed our input is well-formed, let’s move the goalposts a little
closer: rather than discarding "Card {N}: " specifically, we can discard
any character that appears in "Card 0123456789" and is not ":", and then
discard two characters.
That may not seem like a huge improvement, but it allows us to disregard any
character not in those sets, which lets us ask: are there integers x and m
such that the expression (ord(character) + x) % m (where ord is the
Unicode value of a character) is zero for ':' and non-zero for each of
"Card 0123456789"?
A tiny amount brute-force later, we find the answer is yes (x = 0, m = 29):
assert ord(':') % 29 == 0
assert all(ord(c) % 29 != 0 for c in 'Card 0123456789')
This means we can construct a basic block which discards characters until it
reaches a colon (and then calls bb4_read_card_numbers which needs to consume
the space):
def bb3_read_until_colon():
inchr()
push(29)
mod()
not_()
jnz(bb4_read_card_numbers, bb3_read_until_colon)
Parsing numbers
Our next interesting challenge is to parse a one or two digit integer, where
one digit integers are space-prefixed. It would be lovely to use the
instruction that reads numbers, but as noted above, the specification doesn’t
define what state STDIN should be left in, so I am reluctant to write any
program that would need to call any input instruction after using it.
But fear not, we have made a bold assumption that lets us use a dirty trick,
so let’s just do that again. Can we find x and m such that each of the
Unicode characters "0123456789" map to their integer values and ' ' maps
to 0?
assert all(ord(c) % 16 == int(c) for c in '0123456789')
assert ord(' ') % 16 == 0
Huh. That’s a power of two, so we’re just bit-masking to the four
least-significant bits. That feels awfully convenient, very similar to the
case-conversion trick in ASCII ('a-z' can be converted to 'A-Z' and
vice-versa by XORing with 0x20), and seems like the kind of thing my
predecessors would have known about, but I’ve never seen written down
(and nobody pointed me to references when I
asked about it).
If you’ve seen this before, please leave a comment, I’d love to know!
Unfortunately, if we read three characters at a time (space, first maybe-digit,
second digit), the terminating '|' will be in the first maybe-digit space,
which means we actually need to handle the character set " 0123456789|".
Fortunately, ord('|') % 16 == 12, so we can use (ord(c) + 4) % 16 to get 0
when c == '|'.
In the case where the first maybe-digit isn’t '|', we subtract 4 to get its
value, multiply by 10 (to move it to the tens place), read the next character,
modulo by 16 and add to put the second digit in the ones place.
Lists
The next point of interest is how to store card_numbers in our stack.
We will need the length of the list to do various manipulations, so that should
be at the top of the stack, and then we can just put each element of the list
in order: B| list[0] … list[n-1] list_length |T
(where B| and |T indicate the bottom and top of the stack, respectively).
An empty list would just have the list length of zero: B| 0 |T.
As we read each card number, we will need to append it to the card_numbers
list. If we have parsed the card number to the top of the stack, then we merely
need to do some stack manipulation to move the card number into the list
representation:
# STACK: B| card_numbers[0] … card_numbers[n-1] n new_card_number |T
push(2)
push(1)
roll()
# STACK: B| card_numbers[0] … card_numbers[n-1] new_card_number n |T
In this case, we’re using the roll instruction to take the top two values
of the stack and rotate them by one so they get swapped.
Then we just need to increment n so we include new_card_number in the list:
# STACK: B| card_numbers[0] … card_numbers[n-1] new_card_number n |T
push(1)
add()
# STACK: B| card_numbers[0] … card_numbers[n-1] new_card_number n+1 |T
# which is equivalent to
# STACK: B| card_numbers[0] … card_numbers[n-2] card_numbers[n-1] n |T
We will also need to be able to iterate over each element of the list. If we wanted the first element of the list to be at the top of the stack, we can achieve it with the sequence:
# STACK: B| card_numbers[0] … card_numbers[n-1] n |T
dup()
push(1)
add()
dup()
push(1)
sub()
# STACK: B| card_numbers[0] … card_numbers[n-1] n n+1 n |T
roll()
# STACK: B| card_numbers[1] … card_numbers[n-1] n card_numbers[0] |T
Once we are done with this element, we can return the list representation to its canonical state:
# STACK: B| card_numbers[1] … card_numbers[n-1] n card_numbers[0] |T
push(2)
push(1)
roll()
# STACK: B| card_numbers[1] … card_numbers[n-1] card_numbers[0] n |T
dup()
# STACK: B| card_numbers[1] … card_numbers[n-1] card_numbers[0] n n |T
push(3)
push(1)
# STACK: B| card_numbers[1] … card_numbers[n-1] card_numbers[0] n n 3 1 |T
roll()
# STACK: B| card_numbers[1] … card_numbers[n-1] n card_numbers[0] n |T
push(1)
add()
push(1)
# STACK: B| card_numbers[1] … card_numbers[n-1] n card_numbers[0] n+1 1 |T
roll()
# STACK: B| card_numbers[0] … card_numbers[n-1] n |T
If you are still reading this, then either you skipped over that low-level nonsense (fair), read through it and learnt something new (good for you!), or have already dealt with this level of bullshit (my condolences) and thought this was rather ho-hum. If you were in the latter two groups, you’ll be delighted to know that it’s not this simple, as you may have other variables on top of your stack (the number of matches so far, and the current test number), and will need to keep a counter of how far through the list you are. But if you did follow that sequence, those are merely a matter of perseverance.
Structure
Many hours later, I had the high-level algorithm decomposed into basic blocks in my Python representation, and I produced this Graphviz representation:
There are no crossing edges in this layout, which means we could assemble this into an image fairly mechanically: draw the instructions for each basic block vertically, leaving enough space around it for the edges to route the control flow correctly, and then we just need a little extra logic for conditional edges.
One of the things I disliked about using the Piet assembler was the output was sparse and not very artistic, so we’re not going to do that: instead we’re going to try to keep the basic blocks next to each other and keep the image as dense as possible.
Assembly
I used a combination of programs for assembly and debugging:
- GNU Image Manipulation Program for drawing pixels. I created a layer for each basic block: toggling visibility of layers made it easy to match sections of the image to the graph structure, and was useful for isolating sections for debugging.
- Piet Studio, an unreleased Piet debugger I wrote. Like many Piet interpreters, it lets you step through the program showing the current cursor position, direction pointer, codel chooser and stack, but it also lets you manually edit the first three of those (stack editing is still on the backlog 😉).
- npietedit just for figuring out what the colour transitions were for the instructions I needed. These two web-based editors also provide this functionality and may be useful for following along with this section.
- npiet as an independent Piet implementation to verify my program doesn’t rely on bugs in my Piet implementation.
Let’s have a look at how I assembled out the four basic blocks at the top of
my graph: bb0_init_total, bb1_check_eof, bb23_exit, and bb2_not_eof:

We start at the top-left, and the first three codels are bb0_init_total:
we can choose the first arbitrarily (■),
but then we need to push 1, which means our first colour block must only have
one codel (which it does), and we need to shift the colour one darker
(■ → ■).
We next need not, which means we need to shift the colour two darker
(i.e. one lighter) and two hue steps
(■ → ■).
This isn’t our only choice: we could interrupt the flow of colours with a white
codel, which would not be treated as an instruction, but would let us start
again at any colour. This does add two extra codels to the program, so I’ve
only used white colour blocks when they’re needed for the control flow.
The control flow continues on into bb1_check_eof, which ends with not on a
dark blue colour block (■).
We then need to branch: to bb23_exit if the top of the stack is nonzero, or
bb2_not_eof if it is zero. Except I have actually made this easier, and
ensured that whenever we call jnz the top of the stack will always be either
0 or 1 (which is why so many blocks end with not).
There are two instructions for data-driven movement: in this case, we’ll use
pointer (which is one darker and three hue shifts,
so ■ → ■):
which will rotate the direction pointer by the top value on the stack.
If that’s a zero, we’ll keep moving right
(■ → ■ is the pop of bb2_not_eof), otherwise it will be a one, which will start moving us downwards.
I made a few mistakes in Part 1, and one of the big ones was forgetting to
actually output the answer. The program in the graph structure above computes
the answer and leaves it on top of the stack, but bb23_exit should have
included an out instruction.
Unfortunately I had assembled bb23_exit to just exit and put other blocks
around it before I realised this, so I was left the unpleasant task of figuring
out how to retrofit it in. So the instructions in bb23_exit
(■ → ■ → ■)
are out (number) and (uselessly) dup.
The other thing bb23_exit needs to do is terminate the program. From the Piet
specification:
Black colour blocks and the edges of the program restrict program flow. If the Piet interpreter attempts to move into a black block or off an edge, it is stopped and the CC is toggled. The interpreter then attempts to move from its current block again. If it fails a second time, the DP is moved clockwise one step. These attempts are repeated, with the CC and DP being changed between alternate attempts. If after eight attempts the interpreter cannot leave its current colour block, there is no way out and the program terminates.
In this trace from npiet (edited to improve legibility), we can see how that
works in our program: when we enter the final blue block, the direction pointer
is down and the codel chooser is left, so we attempt to move from the codel
marked with 9.0 to the codel below it. That’s black, so we toggle the codel
chooser to right and try again from the codel marked with 9.1. It’s also black,
so we rotate the direction pointer and try again. When the eighth attempt
(9.7) also fails, we realise there’s no way out and the program terminates.
Having dealt with the end of file, let’s take a look at the assembly of
bb3_read_until_colon (bb2_not_eof and bb4_read_card_numbers are also
included to give context):

That’s a big block of dark red. If you recall, we found 29 was the magic number for distinguishing colon/non-colon characters, so we need to push 29 in this block, and you’ll be unsurprised that there are 29 dark red codels in that block. This is not really a mistake, but there are more efficient ways we could have achived the same thing. For example, I could have split this into a sequence of instructions using only 10 codels:
- push 3 (stack:
[3], +3 codels) - dup (stack:
[3 3], +1 codel) - dup (stack:
[3 3 3], +1 codel) - mul (stack:
[3 9], +1 codel) - mul (stack:
[27], +1 codel) - push 2 (stack:
[27 2], +2 codels) - add (stack:
[29], +1 codel)
Anyhow, let’s plow on with the straightforward approach and take a look at how we loop back to the start of the block. Here’s a trace:
We perform the sequence in (character), push 29, mod, not
(■ →
■ →
■ →
■ →
■),
and then we need to go back to the start of bb3_read_until_colon if the top of
the stack is zero, or on to bb4_read_card_numbers if it’s one.
But it makes more sense for the layout if we turn right to get back to the start
of bb3_read_until_colon and do nothing for bb4_read_card_numbers, so we add
another not before we use pointer to change our direction
(■ →
■ →
■).
But there are two more instructions before we go back to the start: push 1 and switch (■ → ■ → ■), what’s with that? Well, when we were on the light red codel at the top right, we were moving right and then hit the black codel to the right, which rotated our direction pointer so we started moving down, but it also flipped our codel chooser from left to right (following the rules quoted above). But it also gets flipped in the white colour block (changing from moving left to up) and the dark yellow colour block (changing from moving up to moving right), which means on the second iteration our codel chooser would be right: then when we exit the big dark red block, we’d be choosing the rightmost codel on the right edge to exit from, which would put us on the light-blue codel, skipping the light red and green codels! So we just flip the codel chooser once more to get us back into the correct state.
This is probably a good time to bring up another mistake I made in constructing Part 1: I used a black background, which means it’s not clear which black codels are load-bearing for the program’s control flow and which are unused. This is good for speed, since I didn’t have to draw in the black codels whenever I need them, but bad for knowing whether I can use adjacent codels for other parts of the program flow, or use for decoration at the end.
There’s not too many things to talk about for Part 1, so here’s my solution:
To help with understanding the high-level control flow, here’s a version where I’ve coloured each basic block a distinct colour and overlaid the npiet trace from running with the example input:
You’ll notice that some parts of the image are coloured but unvisited: these are either the handling for empty lists (which don’t appear in the input) or just decoration.
Part 2
In Part 2, we discover there is no such thing as points. We’re actually winning copies of subsequent scratchcards, and need to count how many we end up with. Here’s the high-level algorithm:
# Number of instances of each scratchcard we've processed so far.
seen = []
# Number of copies for scratchcards yet to be processed.
# (i.e. copies[0] + 1 will be the number of instances for the next scratchcard)
copies = []
for each line in STDIN:
STDIN.discard("Card {N}: ")
# read the winning numbers
card_numbers = []
while STDIN.read(1) == " " (or not "|"):
n = parse_integer(STDIN.read(2))
card_numbers.append(n)
# test how many numbers match
matches = 0
while STDIN.read(1) == " " (or not "\n"):
test_number = parse_integer(STDIN.read(2))
for each card_number in card_numbers:
if card_number == test_numbers:
matches += 1
break
# record the number of instances of this scratchcard in the seen list
instances = 1
if len(copies) > 0:
instances += copies.pop(0)
seen.append(instances)
# make sure copies is long enough
while len(copies) < matches:
copies.append(0)
# add `instances` copies of the next `matches` scratchcards
for each i where 0 <= i < matches:
copies[i] += instances
total = 0
for each instances in seen:
total += instances
print(total)
The first half of the loop is the same as Part 1, so while I did go through
everything again (to be certain of correctness, and add comments about the stack
state to aid in debugging), I was able to copy many of the basic blocks.
You may also notice that the seen list doesn’t need to be a list:
we could just keep a total and add to it instead of appending.
This choice was also made in aid of debugging: if something goes off the rails
and I only notice later, I can look through the list to figure out at which
point it happened.
Decomposing this algorithm into basic blocks was still many hours of effort, but with the aid of rigorous commenting, being able to copy bits from Part 1 and just having more experience, it was a much smoother process than Part 1. Here’s a link to the Python representation, and the Graphviz representation:
This time, I started with a grey background, and marked load-bearing black codels explicitly in their basic block layers. I also wanted to have more room for decoration, so I tried to lay things out so I would get a border around the image, and then put basic blocks inside that. I initially aimed to just leave the “scratch!” box free, but then it became clear I’d have some more space, and so I tried to line up some cells for numbers, which worked out pretty well.
If I turn off the decoration layers, I can get a bare version of the program at the top of this article and get a trace using the example input to show the control flow:
The last step is decoration, and anything can go in the grey areas, so long as it doesn’t change the existing colour blocks by having the same colour adjacent3. I drew in the text and numbers, and then just filled the rest with random greens and blues to be thematic.
As always, code and intermediate stages are in my repository.
-
There are eight possible combinations of the direction pointer and codel chooser, so more sophisticated control flow mechanisms are possible! But we’re going to keep things simple, at least for now… ↩
-
So long as you share my definition of interesting, which… well, I’m not sure how good an idea that is. ↩
-
I was too lazy to do this manually, so all the greens and blues I added are one step away from the correct Piet colours in RGB space. ↩
 flowblok’s blog
flowblok’s blog